On a vu jusque là que les EQ permettent de modifier le niveau sonore à des fréquences précises. Et tout élément sonore peut être représenté par son spectre caractéristique: une sorte de “distribution d’énergie” en fonction de la fréquence. Mais ce spectre est justement composé d’une multitudes de fréquences à des niveaux différents qui vont permettre de définir non seulement la tonalité du son, mais aussi et surtout son timbre.
Le timbre d’un son est un “attribut de la sensation en termes de ce qu’un auditeur peut juger comment deux sons ayant la même intensité et hauteur sont différents”. En effet, le contenu spectral d’un son permet de différencier une note de piano d’une note de violon, pourtant jouée à la même intensité et la même hauteur. Mais le timbre est une notion qui va bien au-delà du simple domaine fréquentiel. Il est aussi dépendant d’autres paramètres, comme notamment l’enveloppe dynamique du son (ce n’est pas l’objet de l’article et j’aurai l’occasion d’y revenir en détail ultérieurement).
Pour l’instant, il est temps de te définir le contenu spectral d’un son. Car, comme on va le voir, cette connaissance est fondamentale à la bonne utilisation des EQ.
Une définition du timbre
1) La fondamentale
C’est la fréquence la plus basse d’un son qui définit le pitch, la hauteur générale du son.
2) Les harmoniques
Ce sont les fréquences en multiple entier de la fondamentale. Par exemple: les harmoniques d’une fondamentale de 100Hz seront à 200, 300, 400, 500Hz, etc…
On peut distinguer les harmoniques paires (dans notre exemple, 200, 400, 600Hz, …) et les harmoniques impaires (300, 500, 700Hz, …). L’oreille n’apprécie pas beaucoup ces dernières: quand trop d’harmoniques impaires sont présentes, on trouve le son “acide” ou “métallique”.
Les harmoniques occupent une place prépondérante dans le son entendu: la fondamentale donnant le pitch, les harmoniques donnent la “couleur” sonore.
Tu peux remarquer que pour passer d’une harmonique à la suivante, on lui ajoute la fréquence de la fondamentale. La progression des harmoniques est donc linéaire (par addition). A ne pas confondre avec la progression des octaves, comme vu dans l’article précédent: chaque octave est à une fréquence double de la précédente. On peut aussi dire qu’elles se succèdent par multiplication avec un facteur de 2. On constate immédiatement que les pas d’une octave à l’autre ne sont pas réguliers, ils vont en augmentant, contrairement aux harmoniques.
Néanmoins, pour définir un son naturel, cela implique bien plus qu’une fondamentale et ses harmoniques. Leur contenu spectral est de loin bien plus complexe. Il faut y intégrer aussi les éléments suivants:
3) Les partiels ("overtones" en anglais)
Ce sont toutes les autres fréquences qui ne sont pas forcément multiples de la fondamentale (une fréquence de 150Hz pour une fondamentale de 100Hz par exemple).
Elles forment un élément du son global qui n’est pas une harmonique du son fondamental (“inharmonique”). C’est le cas des instruments de type cloche et bon nombre de percussions.
Un son de caisse claire produit typiquement beaucoup de bruit mais un pitch peu défini, ce qui est dû à une majorité de partiels.
4) Les formants
Ils représentent des fréquences provoquées par une résonance physique qui ne change pas en fonction de la hauteur du son produit. Les formants contribuent majoritairement à l’empreinte sonore (par exemple, notre habilité à reconnaître la voix de chacun). On parlera de zone formantique pour parler de cette bande de fréquences consécutives, “gonflées” en énergie. Cette répartition de l’énergie joue un rôle important dans la perception timbrale, au même titre que le nombre de composantes dans le spectre, leur répartition ou leur régularité ou non par rapport au modèle harmonique.
Voilà donc une première définition du timbre d’un instrument (du point de vue spectral seulement) défini par la combinaison de ces quatre constituants. C’est ce qui différencie ce qu’on entend de deux instruments jouant la même note. C’est le choix de ces supports sonores et de leur mode d’excitation qui vont déterminer une forme d’onde caractéristique.
Car il y a bien une correspondance entre la forme d’onde et son spectre. Regardons cela sur des ondes basiques:
Exemple avec des ondes simples
Différentes formes d’onde sonnent différemment car leur contenu harmonique est différent.
Maintenant regarde l’analyse fréquentielle pour des ondes simples pour voir pourquoi elles sonnent de telle ou telle manière.
Onde sinusoïdale
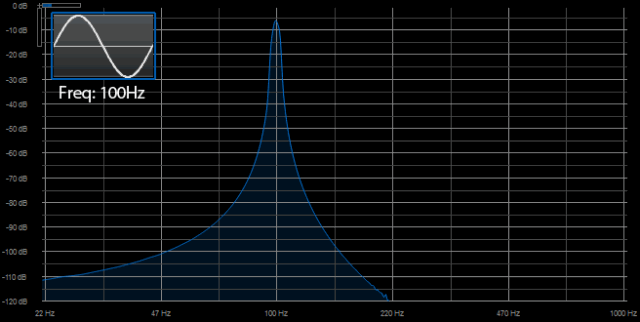
Onde en dents de scie
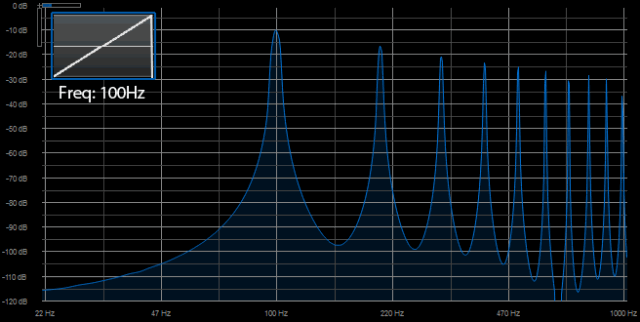
Onde triangle
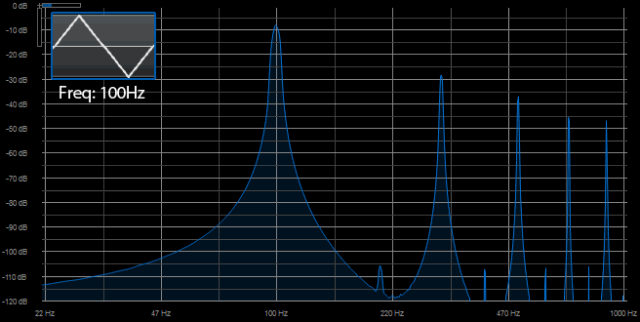
Onde carrée
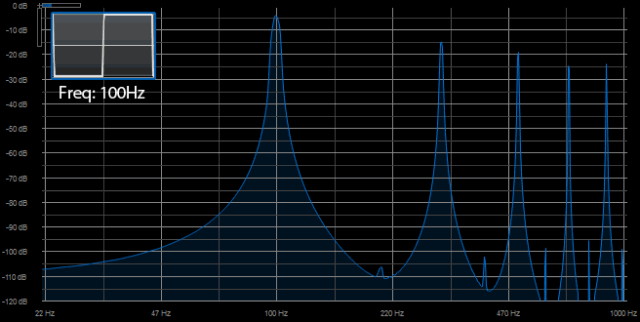
Les ondes Sinus, Carré et Dent de scie constituent la base sonore fondamentale des synthétiseurs (on aura l’occasion d’y revenir).
Fourier: des ondes simples aux ondes complexes
La théorie de Fourier
Il développa la théorie selon laquelle les vibrations complexes peuvent être analysées comme une somme de nombreux signaux simples simultanés.
En d’autres termes, tout signal sonore (onde complexe) périodique (signal musical) est réductible en une addition infinie de sinusoïdes basiques (ondes simples). Il faut bien noter toutefois que cette théorie est valable à l’exception des transitoires (périodes d’établissement et de disparition du son). Mais c’est une notion que je te présenterai plus en détail sur les chapitres de la dynamique du son.
La transformée de Fourier (FT) est la procédure mathématique qui relie une forme d’onde (analogique, continue dans le temps) en sa somme d’une série infinie de sinus élémentaires (discontinue). Autrement dit, elle permet le passage de la forme d’onde à sa représentation spectrale.
L'effet d'ajout d'harmoniques sur la forme d'onde
Mais comment différentes formes d’onde contiennent différentes fréquences, alors qu’elles correspondent à une tonalité commune (une seule fréquence)?
Regardons cela, de manière plus visuelle dans cette vidéo:
L’onde Sinus est une tonalité pure. Elle se trouve être l’élément de constitution de base pour créer d’autres formes d’onde. Tu peux obtenir à peu près n’importe quelle forme d’onde par l’addition d’une série d’ondes sinus à la fréquence, l’amplitude et la phase correctes (c’est le principe de base de la synthèse additive…).
Les ondes en dents de scie ou carrée sont des exemples simples de formes d’onde dérivée de l’onde sinusoïdale additionnée d’autres à des fréquences supérieures (les harmoniques):
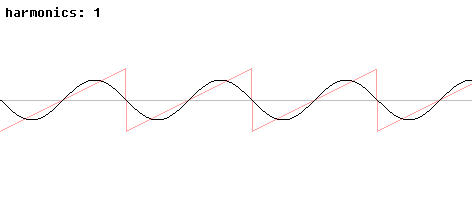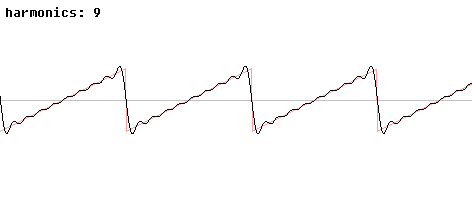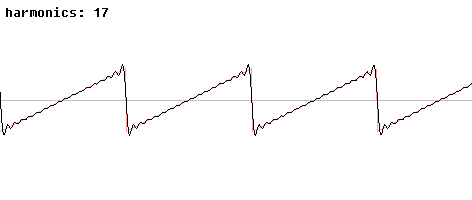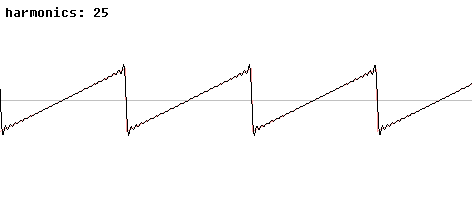
Ce phénomène est ni plus ni moins que la distorsion du son (voir chapitre ultérieur sur la dynamique et la distorsion harmonique).
On a vu que les ondes n’ont pas forcément que des harmoniques, multiples de la fondamentale. Elles possèdent aussi des partiels, fréquences entre ou de manière aléatoire, considérées comme “inharmoniques”. Leurs pics ne tombant pas pile sur un intervalle musical, les inharmoniques sonnent de manière dissonante (comme une cymbale). Juste une touche d’inharmonicité peut ajouter de la “chaleur” à un son, comme dans le cas d’un piano.
Les harmoniques dans l'utilisation des EQ
Mais quel rapport tout cela a à voir avec les EQ me diras-tu?
Et bien la première conséquence est que les fréquences sont toutes importantes pour tous les instruments sur toute la largeur du spectre! On voit bien sur l’image suivante que pour toute une variété d’instruments, leur domaine fréquentiel se chevauche sur une large partie du spectre. Ceci implique de suite que tu devras faire des choix dans la manière de privilégier telle zone fréquentielle pour tel instrument par rapport à un autre.
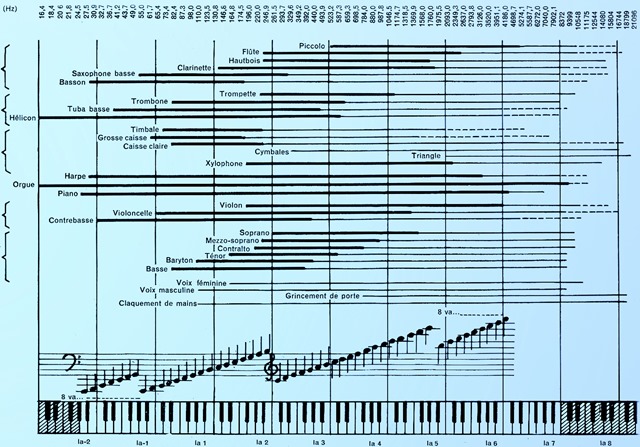
L'exemple du Kick (grosse caisse)
Un Kick typique a une fréquence fondamentale entre 40 et 80Hz.
Une première approche à l’élaboration d’un Kick est de bien régler cette fondamentale afin qu’elle soit dans la même tonalité que le morceau (c’est ce qu’on appelle le tuning).
Ensuite, contrairement à ce qu’on pourrait croire, le Kick est un élément important dans le bas du spectre MAIS AUSSI dans le haut médium voire les aigues! C’est la présence de ces harmoniques qui va donner tout son punch et son attaque.
Effets de masque (ou masquage fréquentiel)
C’est un phénomène bien connu et fondamental à comprendre en mixage audio et pour la bonne utilisation des EQ.
En gros, un signal fort empêche d’entendre (masque) un signal plus faible. Et au niveau fréquentiel, un signal fort masque les fréquences proches. Plus le niveau absolu d’écoute est élevé, plus l’effet de masque s’étend spectralement. Pour avoir un mixage clair, chaque instrument doit avoir “sa place spectrale” (en modifiant ses harmoniques par l’égalisation par exemple).
Pour illustrer cela, prenons l’exemple d’essayer de donner plus de présence à la voix principale quand tu penses que quelque chose d’autre la masque: Essaies d’ajuster les EQ d’autres instruments présents dans une zone de fréquences similaires à la voix (comme le piano, la guitare, la caisse claire…). Si cela n’aide pas, essaies autre chose, peut-être le kick? Si c’est le cas, enlever les fréquences du Kick autour de 2-3 kHz peut rendre la voix plus forte et claire dans le mix.
Domaine sensible du bas médium
On a pu voir également que plus les harmoniques ou partiels s’éloignent de la fréquence fondamentale, plus leur volume respectif décroît globalement. Les fréquences graves sont plus fortes en intensité que les aigues. Ceci entraîne des problèmes courants de masquage dans le bas médium (tu peux voir en détail les caractéristiques de toutes les bandes de fréquence dans le prochain article).
L'effet résiduel
C’est un autre phénomène de la psycho-acoustique bien connu: les partiels supérieurs d’un spectre harmonique fusionnent dans la perception de la hauteur à la fréquence fondamentale, même si celle-ci n’est pas présente. Le cerveau nous fait donc recréer une fondamentale virtuelle du son ou de la note (responsable de la perception de la hauteur)!
C’est la raison pour laquelle on est toujours capable de reconnaître la note Mi la plus grave d’une basse, même si on a effectué un traitement EQ (filtrage au-dessus des 41 Hz) ou que nos enceintes ne sont pas capables de descendre jusqu’à 41 Hz. Ce phénomène a des conséquences très utiles en mixage et seront vus plus en détail.
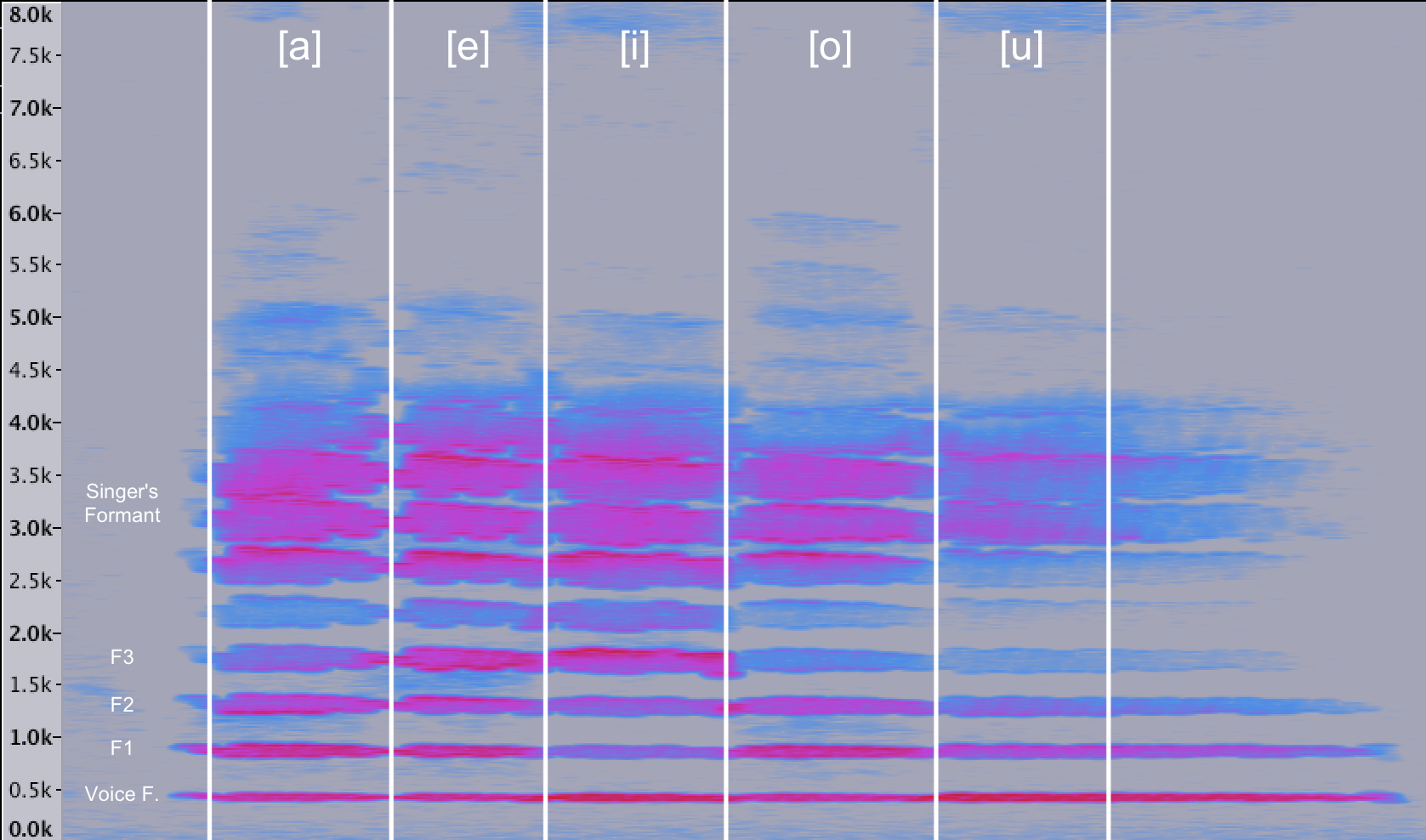
Le formant chantant
Un autre exemple de cet effet est bien connu chez les chanteurs d’opéra.
Problème: L’orchestre joue le plus fort à des fréquences inférieures à la voix et tendent à dominer l’énergie du chanteur au niveau de sa fréquence fondamentale.
Solution: Le chanteur, grâce à sa technique, peut travailler sur son timbre et répartir différemment l’énergie dans le spectre, en la concentrant plus particulièrement autour du formant à 3000 Hz, là où l’oreille est très sensible et réagit aux plus faibles intensités. L’auditeur “rétablit” alors la fréquence fondamentale à partir de la combinaison des partiels supérieurs.
Ce phénomène permet au chanteur qui veut se faire entendre par-dessus un orchestre, de gagner en puissance (ou du moins pour t’en donner le sentiment) sans réellement fournir plus d’énergie. Effort que techniquement il serait bien en peine de fournir… à moins d’y laisser ses poumons!
Catégories
Derniers articles publiés

Tu cherches à maîtriser les outils modernes de la production musicale, traiter ton son comme il le mérite, en finir avec les blocages et finaliser tes morceaux une bonne fois pour toute?
Tu es au bon endroit! Je m’appelle Martin, et je partage avec toi toutes mes connaissances et expérience en ingénierie du son.
De nos jours, il est possible de faire (presque) tout depuis chez soi! Avec les bonnes connaissances, de l’abnégation et de la passion, je suis convaincu que la création musicale est accessible à tous. Je suis prêt à partager ici avec le plus de pédagogie possible, tous les conseils et astuces qui te seront d’une aide précieuse pour arriver à tes fins.


0 Replies to “Comment bien aborder les EQ (2): La perception du timbre”